Phylogentic tree spaces with tropical metric
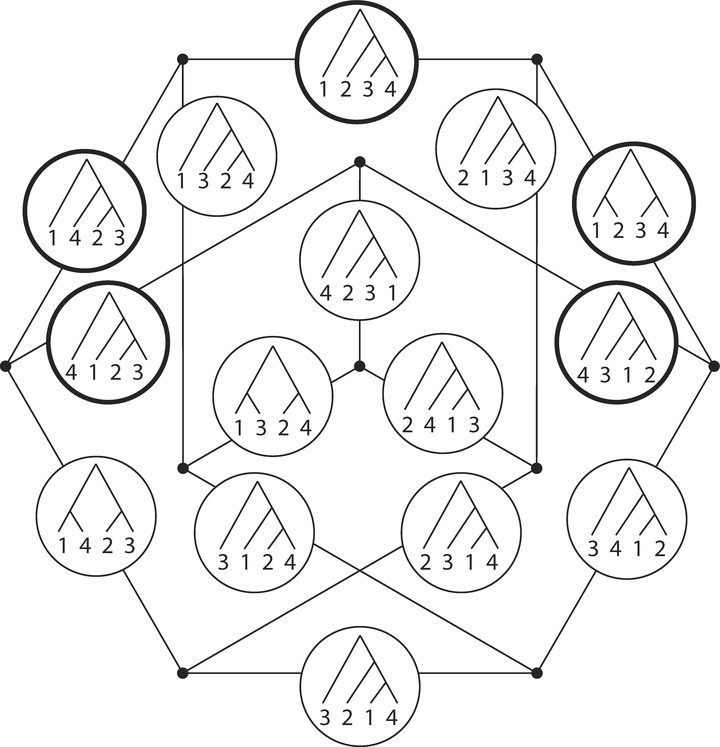space of trees with 4 leaves
Phylogenetic trees are the fundamental mathematical representation of evolutionary processes in biology. Billera-Holmes-Vogtman studied the space of phylogenetic trees with the $CAT-0$ metric, thus the space consists of orthants locally. Computations of distance between two trees and their geodesics could be very complicated in this space.
We propose a novel framework based on tropical geometry that we consider an alternative metric defined on the space, which leads to different geometric properties of the tree space. My collaborators and I study the Fermat-Weber points, Fréchet means, and other objects under this framework, and we hope to apply them to the statistical analysis of evolutionary biological processes represented by phylogenetic trees.
